Non, la célèbre expérience d’Eratosthène ne prouve pas que la Terre est ronde.
En fait, elle est parfaitement compatible avec un modèle de Terre plate.

Mais on sait quand même que la Terre est ronde... grâce à l’expérience d’Eratosthène 🤪

Allez, un thread pour discuter de ça⬇️ https://t.co/0IJPMZujVp

Qu’est-ce que c’est que cette expérience d’Eratosthène ?
Eratosthène est un savant grec qui a vécu vers 200 av. JC.

Il est célèbre pour avoir déduit la circonférence (et donc le rayon) de la Terre, de manière purement géométrique, dans une expérience dont voici le principe : https://t.co/MtNCrNWjAK

On constate que, le même jour (21 juin), les ombres portées par le Soleil ne sont pas les mêmes en différents lieux

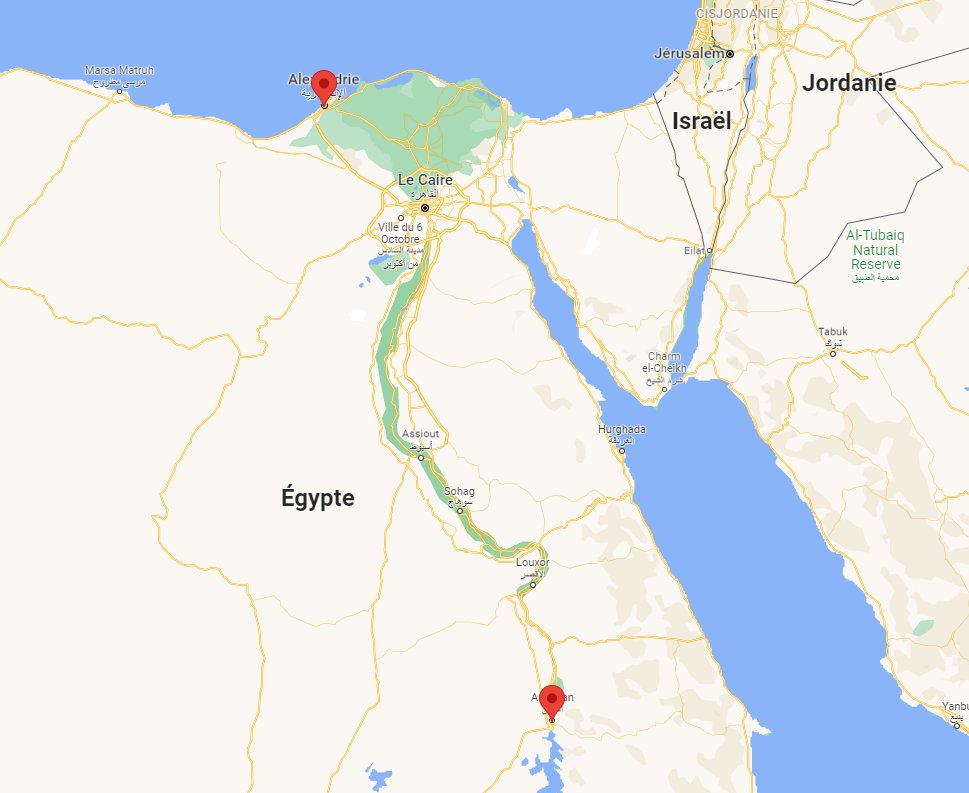
A Syène (Assouan), le Soleil est au zénith. Il n’y a aucune ombre dans un puits

Au même moment, plus au Nord à Alexandrie, les objets ont une ombre portée de 7,2° https://t.co/tgeKJv8OOu

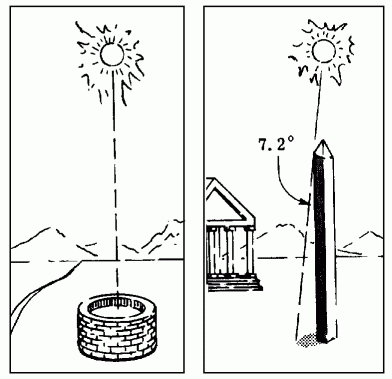
Ça, ce sont les faits.

Pour les interpréter, nous avons besoin d’un modèle mathématique, qui explique ces mesures et en déduit des informations sur le monde.

Dans le modèle d’Eratosthène, la Terre est sphérique, et le Soleil si lointain que ses rayons arrivent parallèles. https://t.co/esdoXF00yL

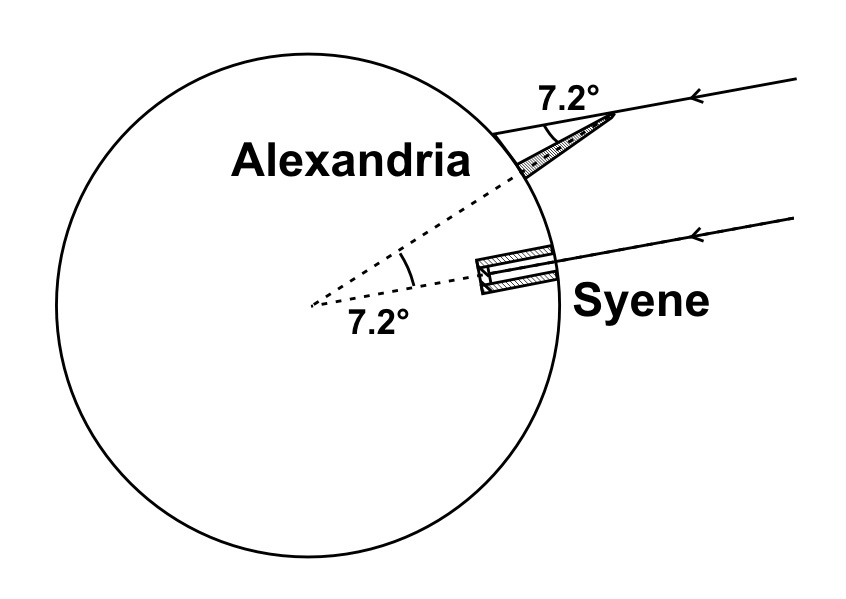
Ce modèle explique bien le fait qu’à Syène, le Soleil soit vu au zénith alors qu’il est observé différemment depuis Alexandrie.

En cause : la rotondité de la Terre, qui fait apparaître le Soleil + ou - haut dans le ciel en fonction de la latitude du lieu où l’on se trouve. https://t.co/RpC6dZd0ND

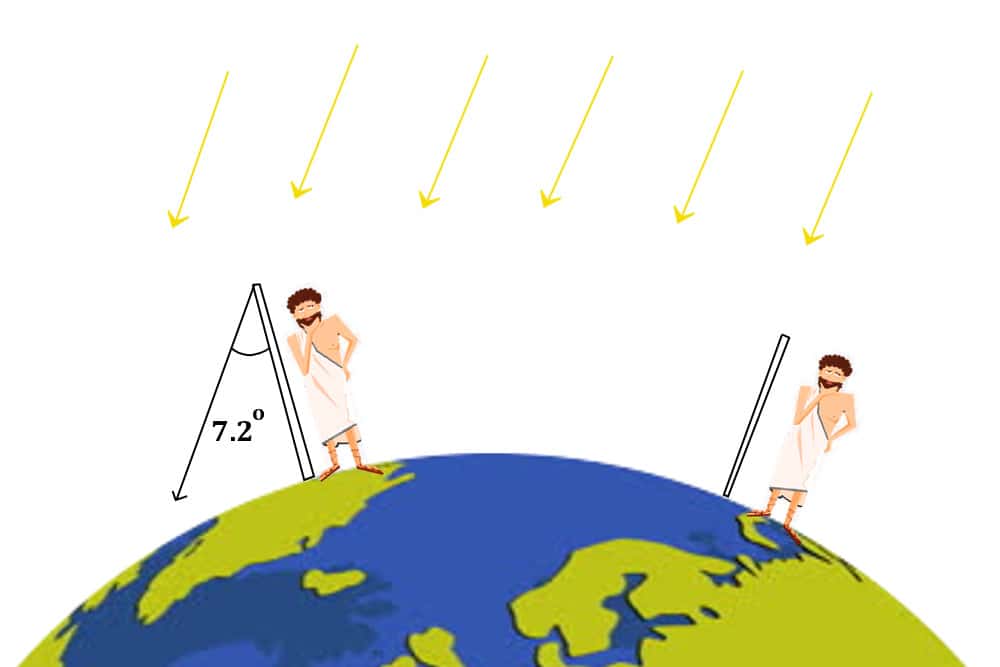
OK pour la partie explicative du modèle.
Mais que peut-on calculer avec ça ?

Eh bien avec ça, on peut calculer assez facilement la longueur de la circonférence de la Terre, sans avoir besoin de la parcourir réellement à pied. https://t.co/YhA7WBeUq4

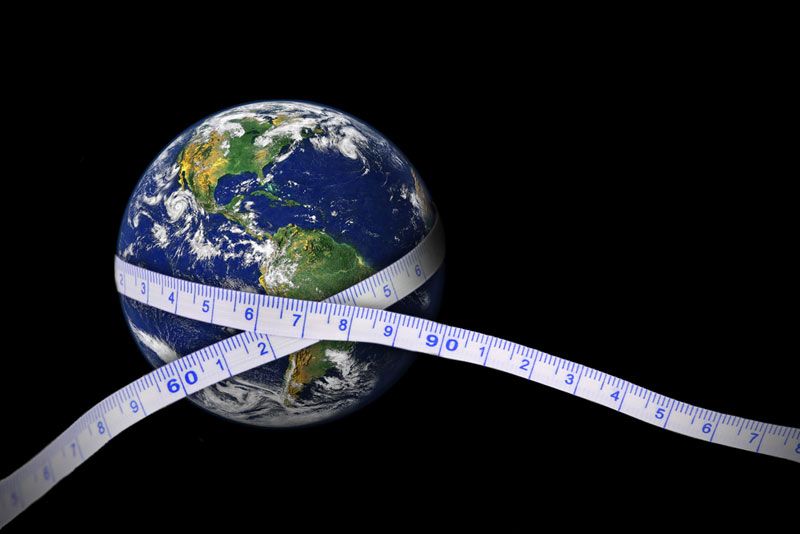
En effet, dans cette expérience, l’angle que font les rayons du Soleil avec le bout de bois à Alexandrie est égal à l’angle entre Alexandrie et Syène, mesuré depuis le centre de la Terre.

Donc on connaît l'angle entre ces 2 villes.
Si on connaît aussi leur distance (...) https://t.co/kizG2TmTnm

(…) on peut calculer la longueur du parcours pour faire un tour entier

Eratosthène estime la distance entre Alexandrie et Syène à 5000 stades (787 km)

Si 7.2° font 787 km, un tour entier (360°) sera parcouru en : 39 350 km

Pas mal pour un périmètre moderne mesuré à 40 075 km. https://t.co/jLHHVhnSaL

Du coup, est-ce que tout ce que nous venons de voir invalide l’hypothèse d’une Terre plate ?

Pas du tout !

Eh bien allons-y, prenons l’hypothèse d’une Terre plate, et voyons si elle s'accorde avec les données observées par Eratosthène : https://t.co/nMSlWXuZ50

On peut tout à fait imaginer un modèle de Terre plate qui correspond exactement aux mesures qu’Eratosthène a effectuées.

Je vous ai fait un schéma (non à l'échelle) ci-dessous pour l’illustrer : https://t.co/UxvTnkS9Ou

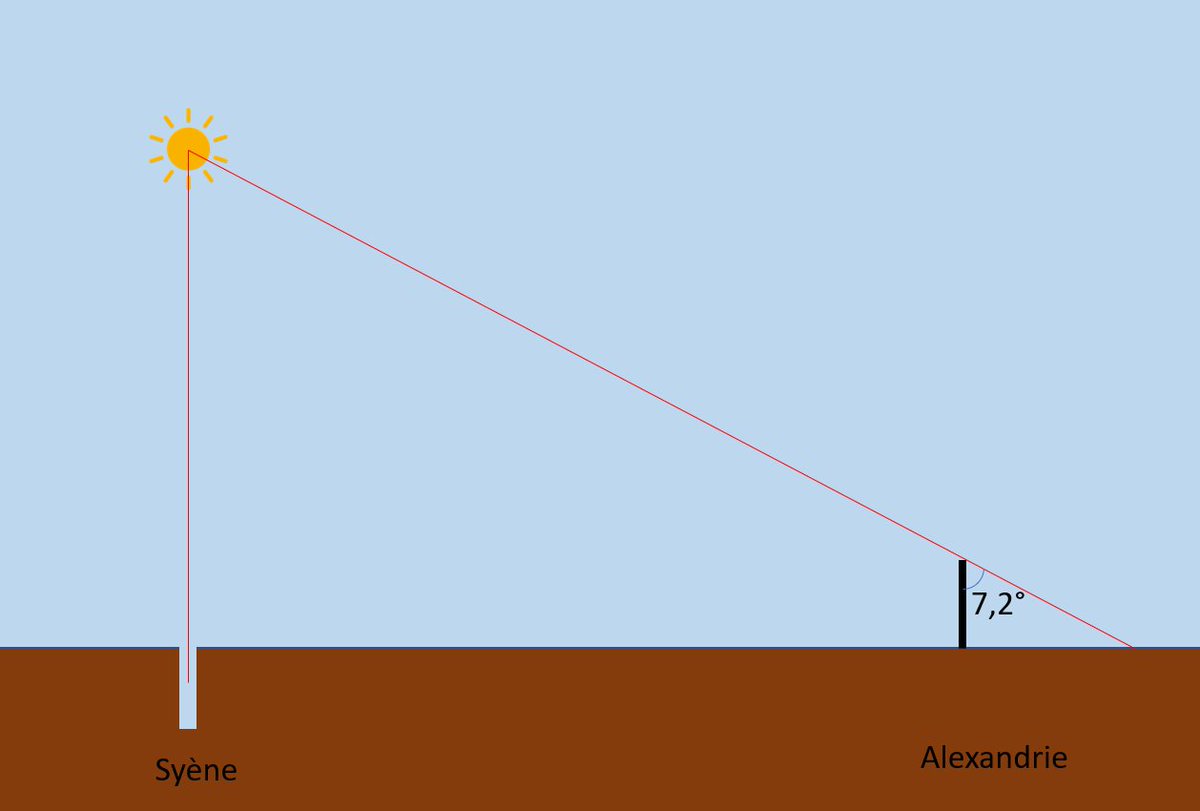
Je le répète, si on s’en tient uniquement aux valeurs d’angles mesurés et de distances estimée par Eratosthène pour les villes de Syène et d’Alexandrie, ce modèle-là est mathématiquement tout aussi valable que l’autre.

Par contre (…)

(…) il ne permettra pas de calculer la même chose.
Inutile de s’en servir pour estimer le "périmètre" ou le "rayon" de la Terre (puisqu'elle est plate).

Par contre, ce nouveau modèle nous donne directement accès à une autre valeur intéressante : la distance du Soleil à la Terre

En effet, nous sommes dans un triangle rectangle dont on connaît un angle et la longueur d’un côté (la distance Syène-Alexandrie, toujours égale à 5000 stades).

Il est alors très facile de déterminer la distance du Soleil au-dessus de Syène, qui est alors de 6230 km. https://t.co/gWgu7u3A1x

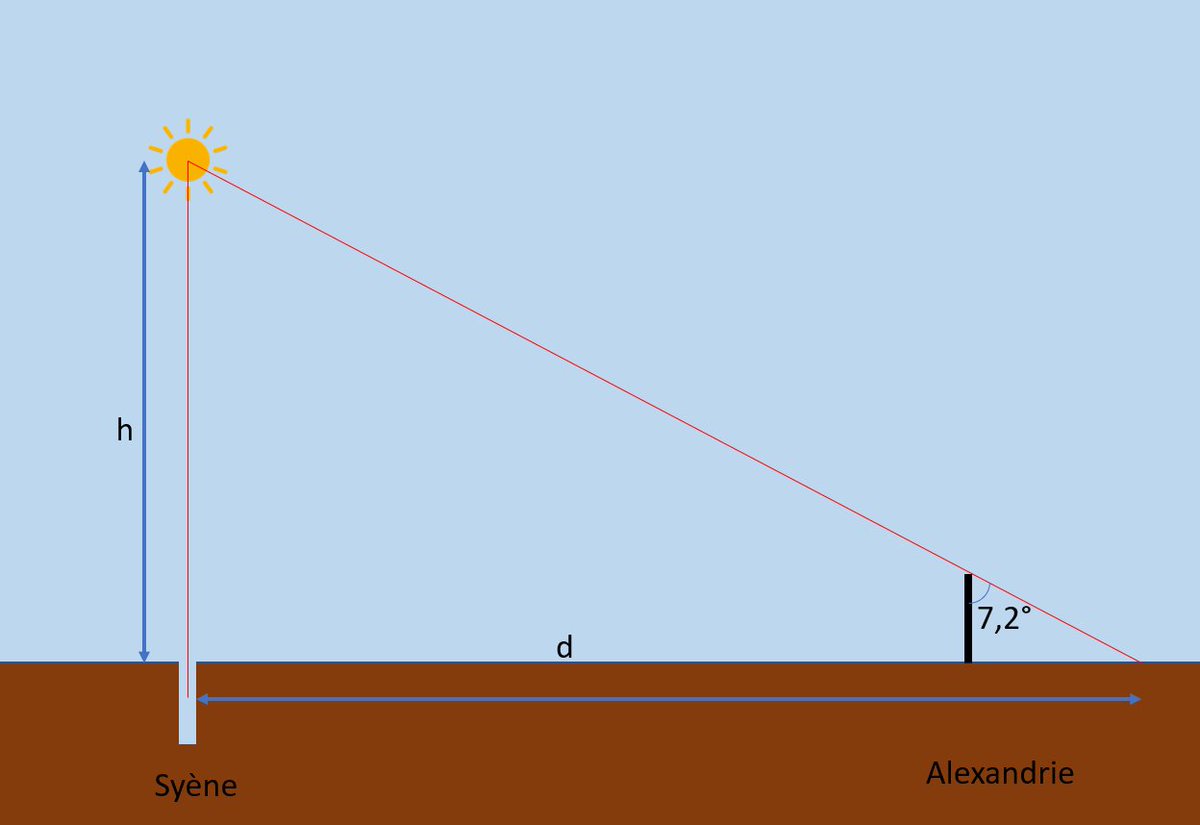
Nous avons donc 2 modèles, parfaitement cohérent d’un point de vue mathématiques, qui, chacun, permet de calculer un paramètre impossibles à mesurer par Eratosthène pour les vérifier : soit le périmètre de la Terre (Terre sphérique), soit la distance Terre-Soleil (Terre plate). https://t.co/i0CgVfu60y

La question est, bien sûr : "comment départager ces 2 modèles ? "

La Terre est-elle finalement plutôt plate ou plutôt sphérique ?

Eratosthène a-t-il échoué dans sa tentative de prouver la rotondité de la Terre ?

Nous aurait-on menti ? https://t.co/XDG8BHWHh5

Ne vous y trompez pas. L’expérience d’Eratosthène peut effectivement prouver la rotondité de la Terre, mais pas dans les conditions "historiques".

La véritable différence entre les deux modèles apparaît dès qu'on fait des mesures à partir de... 3 villes.

Démonstration: https://t.co/To7RGZBjGE

Pour cette nouvelle expérience, je nous ai choisi 3 villes situées sur le même méridien (pour qu'elles voient culminer le Soleil au même moment dans le ciel, c'est plus simple pour les calculs).

Nous avons donc:

- Fresnillo (Mexique)
- Sidney (Nebraska, USA)
- Melville (Canada) https://t.co/bk2WYTM3cj

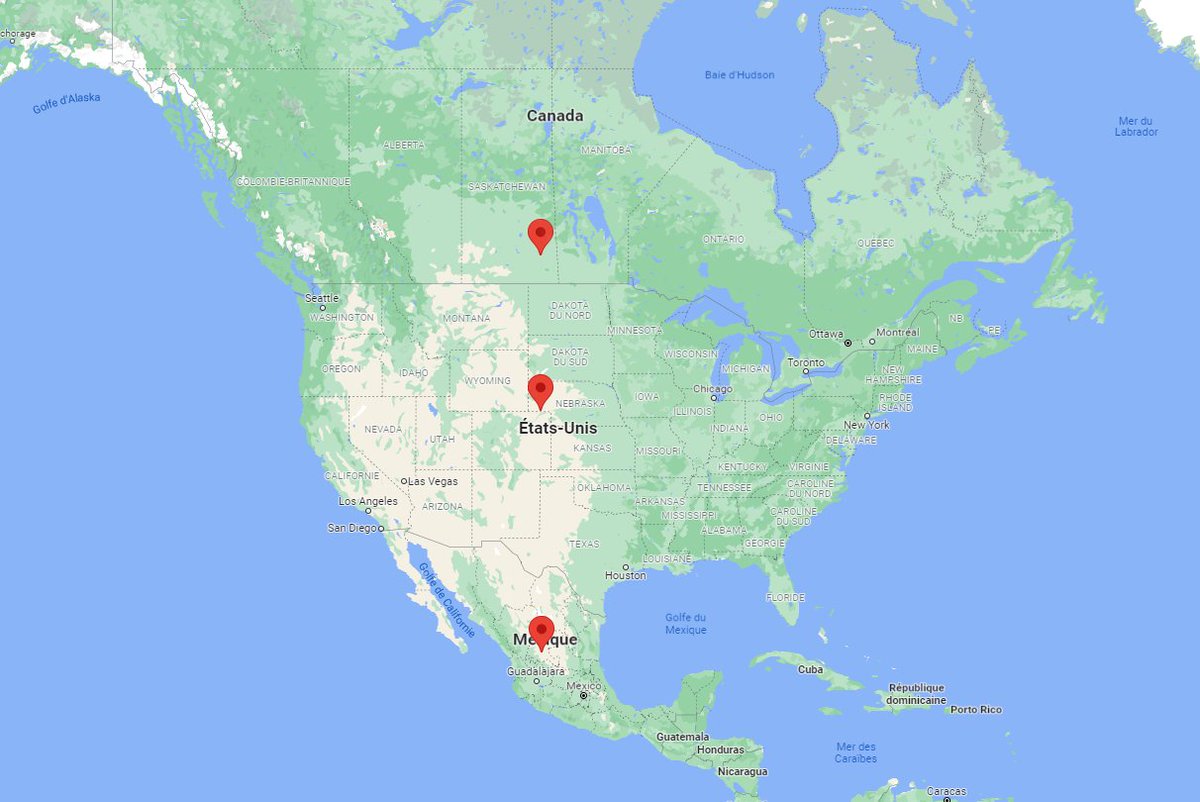
Les distances entre les villes sont données par n’importe quel site de calcul routier/géographique.

Fresnillo-Sidney : 1998 km
Sidney-Melville : 1088 km

La hauteur du Soleil le 21 juin est donnée par votre logiciel astro préféré.

Fresnillo : 90°
Sidney : ~72°
Melville : ~62,2°

On se retrouve donc dans la même situation qu'Eratosthène, avec une ville qui, le jour du solstice d'été, voit le soleil passer au zénith, et 2 villes plus au Nord qui, le même jour à la même heure, voient le Soleil plus bas dans le ciel.

Comparons maintenant nos 2 modèles :

Dans le modèle d’Eratosthène, on le rappelle, la différence de hauteur du Soleil dans le ciel vue depuis chaque ville est due à la rotondité de la Terre. https://t.co/Hymy9ZiCTz

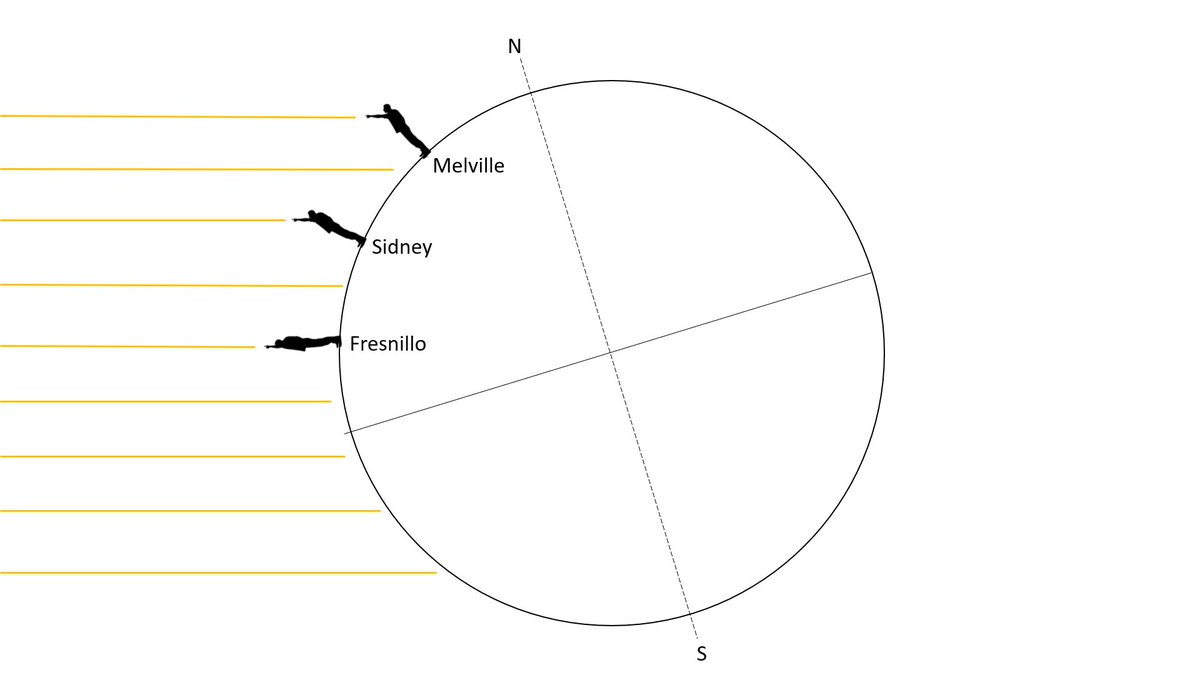
Maintenant prenons les villes 2 à 2 et faisons de nouveau le même calcul que celui que nous avons fait plus tôt avec Alexandrie et Syène, mais cette fois-ci avec les angles et les distances correspondant à ces 3 villes.

Peut-on de nouveau calculer la circonférence terrestre ?

Si on fait le calcul entre la ville de Fresno et de Sidney, on obtient un périmètre de la Terre de 40 071 km

Pour Fresno et Melville : 39 963 km

Pour Sidney et Melville : 39 762 km

La variation entre les différents résultats est de moins de 0.8%

Pourquoi ces variations ?

1) j'ai fait de petits arrondis dans la mesure de la hauteur du Soleil (et ces calculs sont très sensibles au nombre de décimales utilisé).

2) la Terre n'est pas parfaitement sphérique (contrairement à notre modèle) mais légèrement aplatie aux pôles.

Faisons maintenant les calculs avec le modèle de la Terre plate.

Comme plus haut, nous allons calculer la distance du Soleil à la Terre, pour différents couples des 3 villes disponibles.

Cette valeur ne devrait pas non plus beaucoup varier d’une mesure à l’autre.

Allons-y !

Dans le modèle de la Terre plate, les angles mesurés correspondent au fait que le Soleil se trouve proche de la Terre.

Il est donc vu sous des angles différents lorsqu’on se trouve à des positions différentes (on appelle ça l’effet de parallaxe).

(figure non à l'échelle) https://t.co/i4VPdH7pXw

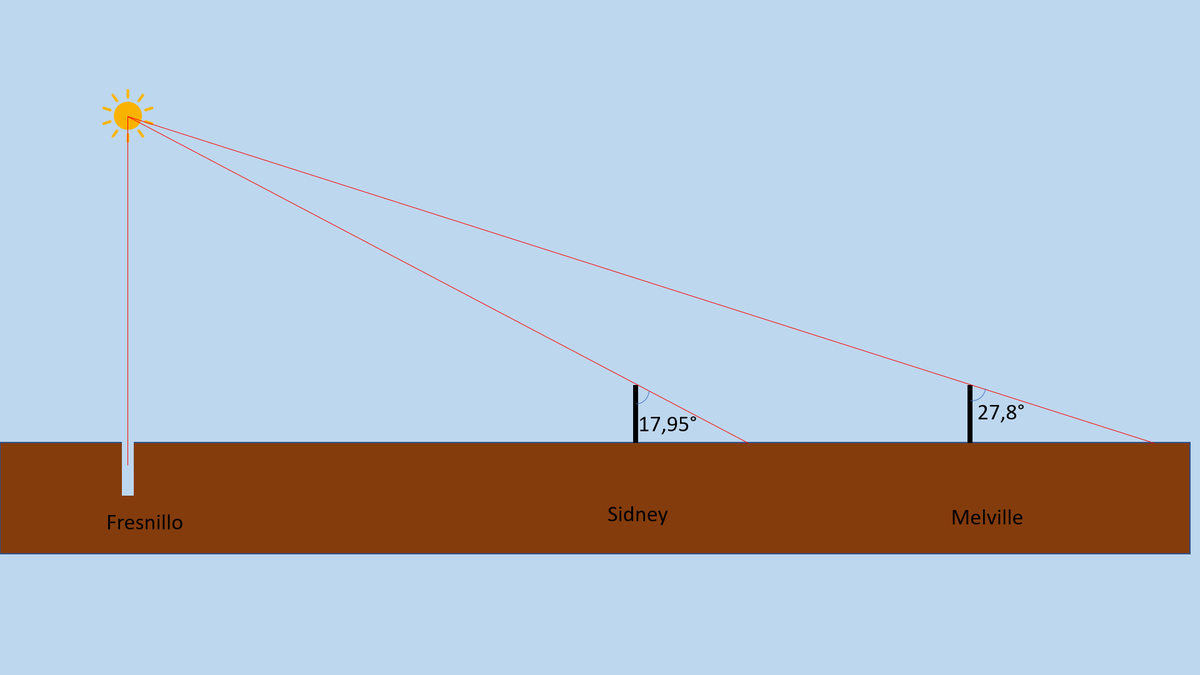
Passons maintenant aux calculs.

Lorsqu’on prend les mesures d’angles et de distance entre les deux villes de Fresillo et de Sidney, dans le modèle de la Terre plate, on trouve que le Soleil se trouve au-dessus de Fresnillo (logique) à une altitude de 6168 km. https://t.co/Siao3ont5Z

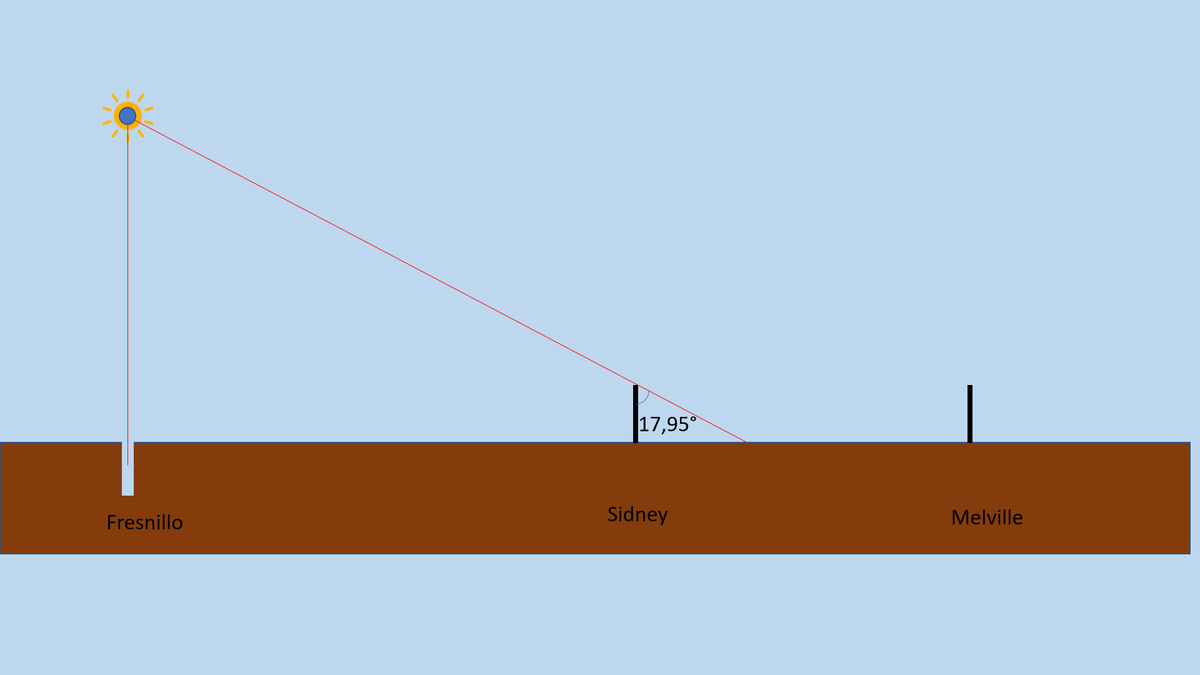
Lorsqu’on fait le même calcul entre la ville de Fresnillo et de Melville, la distance du Soleil à la Terre, au-dessus de Fresnillo, tombe soudainement à 5853 km.

Le Soleil perd 314 km d’altitude, ce qui fait tout de même une variation de 5% entre ce résultat et le précédent. https://t.co/D709N2fCfY

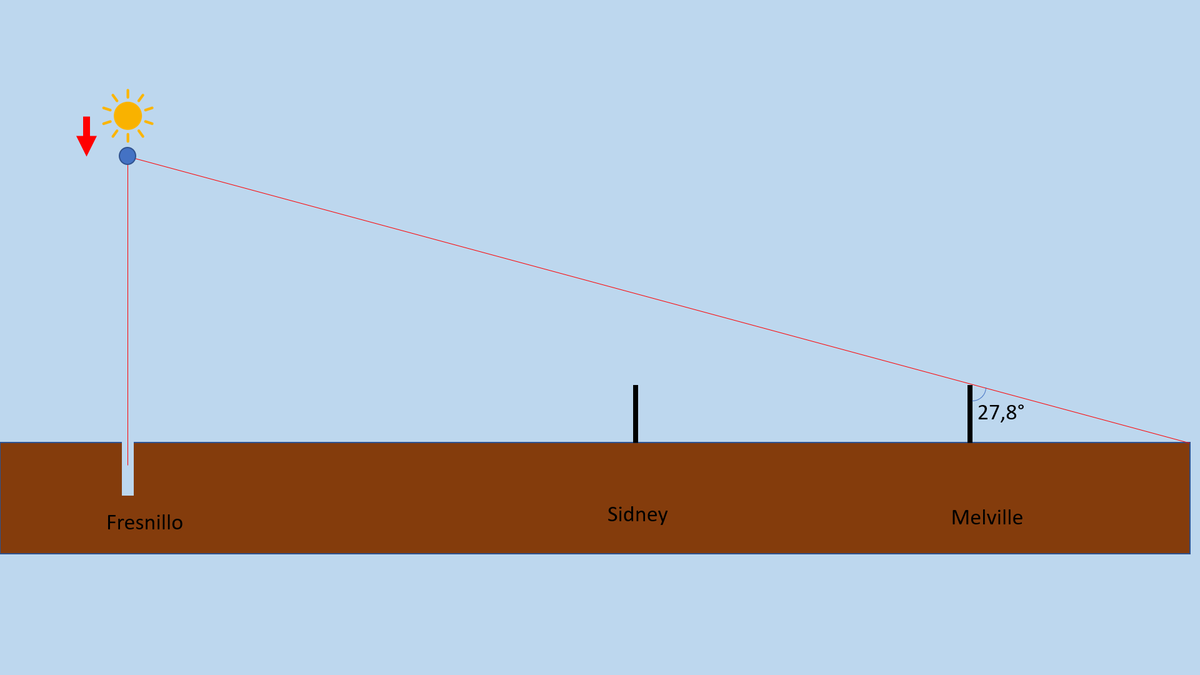
Faisons maintenant le dernier calcul de la position du Soleil à partir des villes de Sidney et Melville.

Cette fois-ci, non seulement le Soleil perd 815 km d’altitude (13% de variation par rapport au 1er calcul), mais en plus, IL SE DÉCALE DE 264 km VERS LE NORD ! https://t.co/PqjeBZQD69

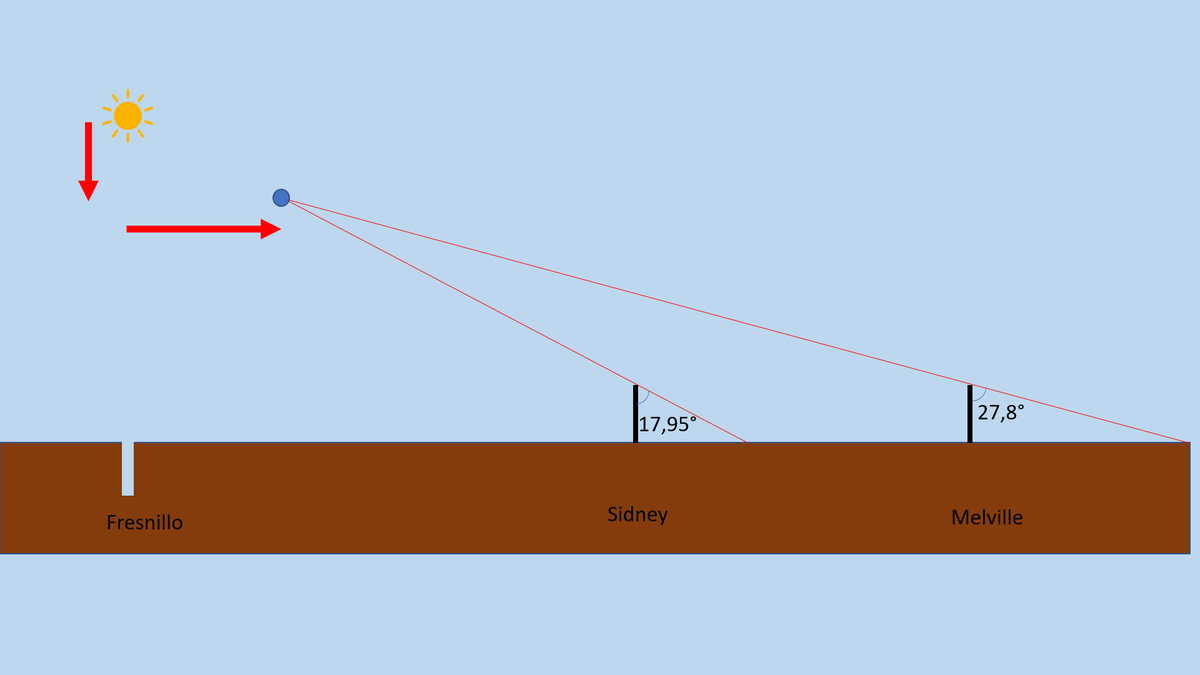
Et c’est ça, le principal problème de ce modèle.

Peu importe qu’il postule que le Soleil survole la Terre à 6 000 km, le souci est que ce modèle n’est même pas consistant avec lui-même, donnant des résultats différents aux mesures du même paramètre (la position du Soleil). https://t.co/6KmnPPDgdj

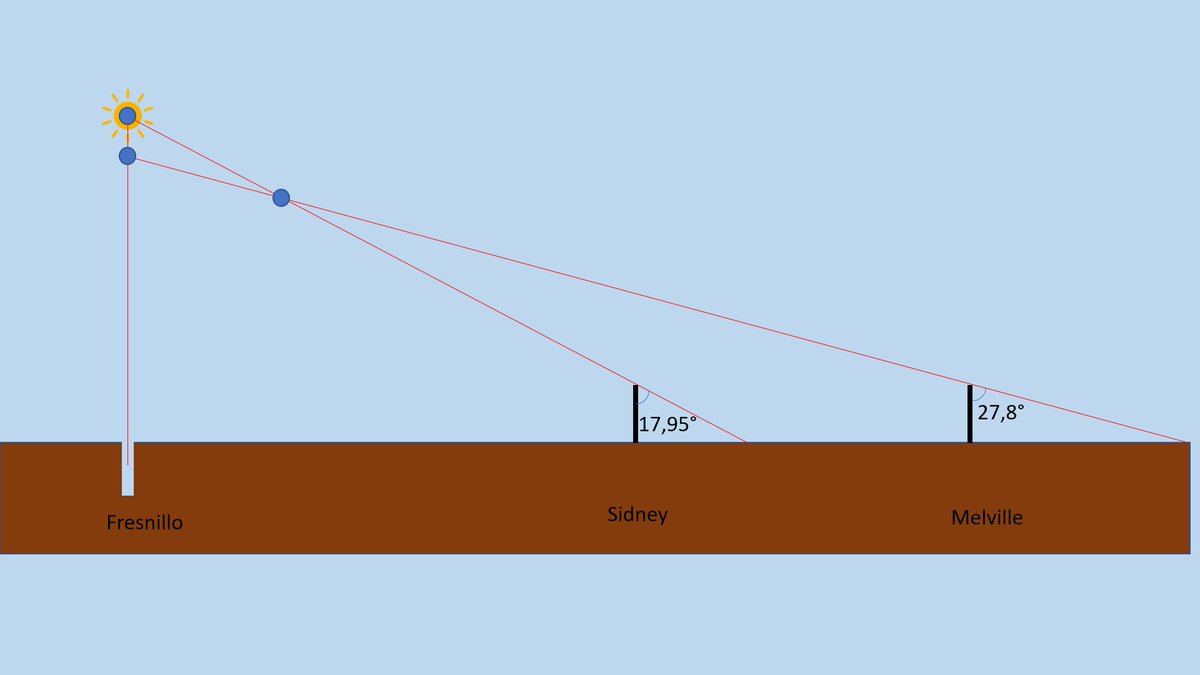
Voilà en quoi le modèle d'Eratosthène est bien plus solide que celui de la Terre plate : parce que plus on accumule les observations, partout dans le monde, plus le résultat est répété et confirmé.

Et c'est exactement l'inverse qui se passe pour le modèle de la Terre plate. https://t.co/MgOYZrr7Fm

Par contre, et c’était le point de ce thread, il est exact de dire qu’avec seulement deux points de mesure (dans seulement 2 villes), c’est-à-dire dans les conditions expérimentales d’Eratosthène, les deux modèles fonctionnent aussi bien l’un que l’autre.

En science, pour valider un modèle, on multiplie les observations, pour tester sa solidité et réduire les barres d’erreur.
Et ce test, le modèle de la Terre plate ne le passe pas.

Voilà (entre autre) pourquoi la Terre plate est scientifiquement abandonné depuis longtemps.

Merci de m’avoir lu.

J’espère que ce thread vous aura intéressé.
Bonne continuation, et prenez soin de vous.